15 Oplosser
De Oplosser is een hulpprogramma (invoegtoepassing) binnen Excel om optimalisatieberekeningen uit te voeren. Bij zo’n berekening wil je een optimale waarde voor een formule in een bepaalde cel vinden, meestal een minimum of een maximum en soms een heel specifieke waarde.
- doelcel
- Dit is de de cel met een formule waarvoor je de optimale uitkomst wilt vinden.
- variabele cellen, veranderende cellen, beslissingsvariabelen
- Dit zijn de cellen die de uitkomst van de formule bepalen. Door de waarden hierin te wijzigen, verandert ook de uitkomst van de formule.
- restricties, randvoorwaarden, constraints
- Dit zijn beperkingen die voor de variabele cellen gelden, deze kunnen vaak niet alle mogelijke waarden aannemen en zijn aan grenzen gebonden.
Oplosser heeft meer mogelijkheden dan Doelzoeken om “Wat-Als” analyses uit te voeren en is veel breder inzetbaar. Oplosser past de waarden van de veranderende cellen aan binnen de grenzen van de randvoorwaarden om tot de optimale oplossing van de doelcel te komen.
15.1 Beschikbaarheid Oplosser
De Oplosser is een zogenaamde invoegtoepassing welke niet standaard via het menu van Excel beschikbaar is. Wanneer de Oplosser nog niet op het lint aanwezig is dan moet deze eerst geactiveerd worden. Dit is een eenmalige actie.
Controleer eerst of Oplosser op het lint beschikbaar is. Zoja, dan kun je deze taak overslaan. Kies tab Gegevens, kijk of de groep Analyse bestaat en zoja of hierin de Oplosser aanwezig is.
Taak 15.1
Kies Bestand > Opties > Invoegtoepassingen. Er verschijnt een lijst met Microsoft Office Invoegtoepassingen.
Selecteer Excel-invoegtoepassingen onder in het scherm in het vak Beheren.

Klik op Start…. Er wordt nu een lijst met beschikbare invoegtoepassingen getoond.
Vink het selectievakje Oplosser-invoegtoepassing aan en klik op OK.
- Controleer opnieuw of Oplosser nu op het lint beschikbaar is.
15.2 Opzetten optimalisatiemodel
Om een optimalisatieberekening uit te kunnen voeren moet je eerst een geschikt berekeningsmodel opzetten. Dat is meestal veel moeilijker dan het gebruik van de Oplosser zelf. Het maken van zo’n model wordt uitgelegd aan de hand van de casus WeatherLeather.
15.2.1 Case beschrijving
WeatherLeather, een fabrikant van dure leren jacks, heeft twee ontwerpen gemaakt voor het nieuwe seizoen, een lang jack en een kort jack. Voor het maken van een kort jack is 1 uur werktijd op de snijafdeling en 3 uur werktijd op de naaiafdeling nodig. Voor een lang jack zijn deze tijden respectievelijk 2 uur en 4 uur. De hoeveelheid werktijd op de snijafdeling en de naaiafdeling is beperkt. De beschikbare capaciteit op de snijafdeling is 32 uur per week en op de naaiafdeling 84 uur per week. De marktvraag naar lange leren jacks is beperkt. Niet meer dan 12 lange leren jacks kunnen per week afgezet worden. Voor de korte jacks geldt dat alle gemaakte jacks verkocht kunnen worden. Er wordt niet op voorraad geproduceerd. De winst op een kort jack is 90 Euro en op een lang jack 144 Euro.
Hoeveel jacks van elk type moeten per week gemaakt worden om een zo groot mogelijke winst te krijgen?
15.2.2 Begrijp probleem
Deze stap lijkt zo vanzelfsprekend dat het misschien nauwelijks de moeite waard lijkt deze te vermelden. Toch is het van belang om hier bij stil te staan voordat je begint met het formuleren van de doelcel, de veranderende cellen en de restricties. Wanneer je het probleem niet volledig begrijpt loop je de kans op onjuiste formuleringen in het model. De probleemstelling in dit voorbeeld is vrij eenvoudig:
Hoeveel korte en lange jacks moet je per week produceren om een maximale winst te krijgen, terwijl je niet meer dan 32 uur snijtijd en 84 uur naaitijd tot je beschikking hebt.
15.2.3 Beslissingsvariabelen
Stel de beslissingsvariabelen vast. Dit zijn de veranderende cellen waarvoor je een waarde moet vaststellen die tot het optimale resultaat leiden. In dit voorbeeld zijn er twee beslissingsvariabelen welke gemakshalve met een letter worden aangeduid:
- \(\mathrm{K}\) = aantal korte jacks per week
- \(\mathrm{L}\) = aantal lange jacks per week
15.2.4 Doelfunctie
Er moet een formule bepaald worden waarvan de uitkomst de optimale waarde moet krijgen. In deze formule komen de beslissingsvariabelen voor. In dit voorbeeld is de doelfunctie de behaalde winst per week en deze hangt af van het aantal geproduceerde korte jacks (\(\mathrm{K}\)) en lange jacks (\(\mathrm{L}\)):
\(\mathrm{Winst = 90 \times K + 144 \times L}\) (deze moet gemaximaliseerd worden)
Bij wat ingewikkelder modellen is het soms lastig om het probleem zo te formuleren dat één doelfunctie verkregen wordt. Dan kan het gebeuren dat de beslissingsvariabelen niet rechtstreeks in de doelfunctie voorkomen, maar via een omweg. In de doelfunctie komen dan variabelen voor waarvan de waarden uiteindelijk weer afhangen van de beslissingsvariabelen.
15.2.5 Constraints
Meestal zijn er beperkingen voor de waarden die de beslissingsvariabelen kunnen aannemen. Deze beperkingen moeten opgespoord en geformuleerd worden.
In dit voorbeeld zijn drie restricties die rechtstreeks uit de casus komen, de beperkte capaciteiten voor de snij- en naaiafdeling en de marktvraag voor de lange jacks.
Daarnaast zijn er vaak algemene restricties die te maken hebben met het gegevenstype van de beslissingsvariabelen. Zo moeten in dit voorbeeld de twee beslissingsvariabelen, het aantal geproduceerde jacks, altijd positieve en gehele getallen zijn. In Excel heet een geheel getal een integer.
Dit alles leidt tot de formulering van de volgende restricties:
- Restrictie snijtijd per week: \(\mathrm{1 \times K + 2 \times L \le 32}\)
- Restrictie naaitijd per week: \(\mathrm{3 \times K + 4 \times L \le 84}\)
- Restrictie marktvraag lange jacks: \(\mathrm{L \le 12}\)
- Restricties positieve waarden: \(\mathrm{K \ge 0}\) en \(\mathrm{L \ge 0}\)
- Restricties gehele waarden: \(\mathrm{K = integer}\) en \(\mathrm{L = integer}\)
15.2.6 Model in Excel
Het model moet nu in Excel worden ingevoerd zodat het probleem straks met Oplosser kan worden opgelost. Een manier waarop dat kan is in Figuur 15.4 te zien.
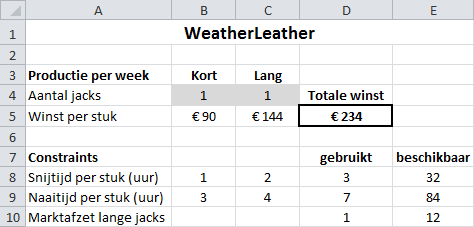
Er is niet één goede manier om een dergelijk model in Excel te bouwen. Wel zijn er een aantal richtlijnen te geven. Deze richtlijnen worden hierna besproken aan de hand van Figuur 15.4. Je kunt uiteraard het model met behulp van deze aanwijzingen en de afbeelding nabouwen, maar het is ook in het bestand WeatherLeather.xlsx beschikbaar.
15.2.7 Richtlijnen voor een Oplossermodel in Excel
Organiseer de gegevens op een logische en overzichtelijke wijze en zet voldoende toelichtende tekst in de buurt van de cellen met getallen en formules. Een model wordt later vaak in rapportages gebruikt en dan moet duidelijk zijn wat alles voorstelt en waar het om draait. Markeer de cellen met de beslissingsvariabelen (B4 en C4) en de doelfunctie (D5) zodat ze gemakkelijk herkend worden. Zet de constraints in een afzonderlijk deel.
Zet elke beslissingsvariabele in een aparte cel en geef ze een startwaarde. Zo staat in het voorbeeld het aantal geproduceerde korte en lange jacks in respectievelijk cel B4 en cel C4. Als startwaarde is in beide gevallen 1 gebruikt. Hierdoor kan in ieder geval de juistheid van de formules gecontroleerd worden.
Maak een formule voor de doelcel. In D5 is de formule
=B5*B4+C5*C4.Maak voor elke restrictie een formule in een aparte cel en zet in de cel rechts er van de grenswaarde van de restrictie.
| cel | formule | toelichting |
|---|---|---|
| D8 | =B8*B4+C8*C4 |
berekening totale snijtijd |
| D9 | =B9*B4+C9*C4 |
berekening totale naaitijd |
| D10 | =C4 |
aantal lange jacks |
15.2.8 Randvoorwaarden in Oplosser
Het dialoogscherm in Oplosser waarmee je randvoorwaarden toevoegt ziet eruit zoals in Figuur 15.5.
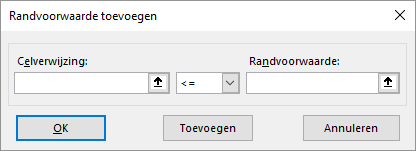
Elke randvoorwaarde bestaat uit drie onderdelen: een Celverwijzing, een relatie en een Randvoorwaarde.
- Celverwijzing
- Celadres of naam of cellenbereik waarvan je de waarden wilt beperken. Je kunt een enkele cel of een bereik gebruiken, maar niet meerdere bereiken.
- Relatie
-
Mogelijke operatoren:
<=,=,>=,geh,binofdif. -
gehwordt later in het model weergegeven alsgeheeltallig. De waarden in de celverwijzingen moeten dan gehele getallen zijn, binnen een bepaalde kleine tolerantie (vastgelegd met de Precisie van randvoorwaarde in de opties van de Oplosser).
-
binwordt later in het model weergegeven alsbinair. De waarden in de celverwijzingen moeten of 0 of 1 zijn. Deze mogelijkheid kun je dus ook gebruiken voor “ja/nee” beslissingen.
-
difwordt later in het model weergegeven alsAllDifferent. De waarden in alle celverwijzingen moeten verschillend zijn.
- Randvoorwaarde
- Een getal, celverwijzing, naam of een formule waaraan voldaan moet worden.
15.3 Implementatie model
Bij de casus WeatherLeather moet de winst gemaximaliseerd worden.
Taak 15.2 Bestand: WeatherLeather.xlsx
Open het bestand.
Selecteer de doelcel D5.
Kies tab Gegevens > Oplosser (groep Analyse).
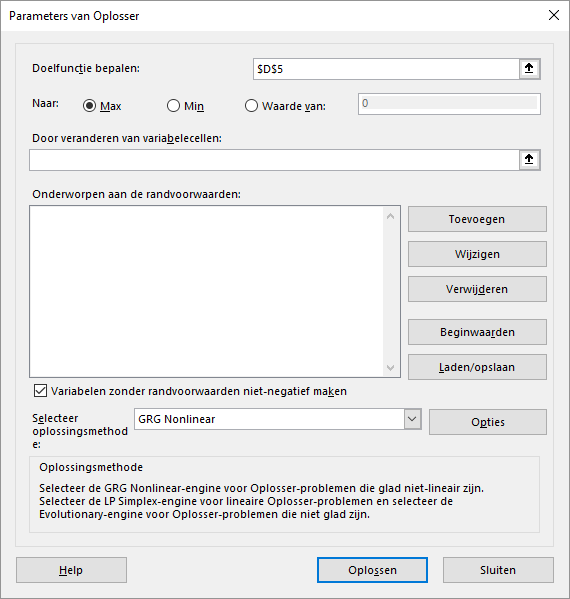
Controleer het volgende:
- Doelfunctie bepalen:
$D$5 - Naar:
Max
- Doelfunctie bepalen:
Klik in het vak Door veranderen van variabelecellen en selecteer daarna in het werkblad de cellen B4:C4. Excel maakt hier dan van
$B$4:$C$4.Klik in het gedeelte voor randvoorwaarden op Toevoegen. Het dialoogvenster Randvoorwaarde toevoegen verschijnt (zie Figuur 15.5.
Voer als randvoorwaarde in
D8 <= E8en klik op OK.
Het dialoogvenster Parameters Oplosser verschijnt weer en Excel heeft de eerste randvoorwaarde omgezet in $D$8 <= $E$8.
Klik op Toevoegen.
Voer als randvoorwaarde in
D9 <= E9en klik nu op Toevoegen.
Het lege dialoogvenster Toevoegen verschijnt weer. Je krijgt nu niet te zien dat Excel de tweede randvoorwaarde heeft toegevoegd.
Voer als randvoorwaarde in
D10 <= E10en klik op Toevoegen.Voer als randvoorwaarde in
B4:C4 >= 0en klik op Toevoegen.Voer als randvoorwaarde in
B4:C4 geh. Excel plaatst nu automatischgeheeltalligin het vak Randvoorwaarde.Alle restricties zijn nu toegevoegd. Klik op OK.
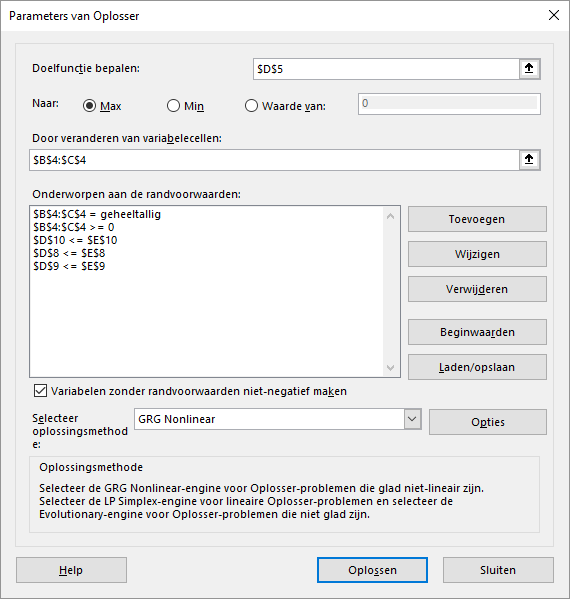
- Klik op Oplossen. Na korte tijd verschijnt het resultaatvenster van de Oplosser.
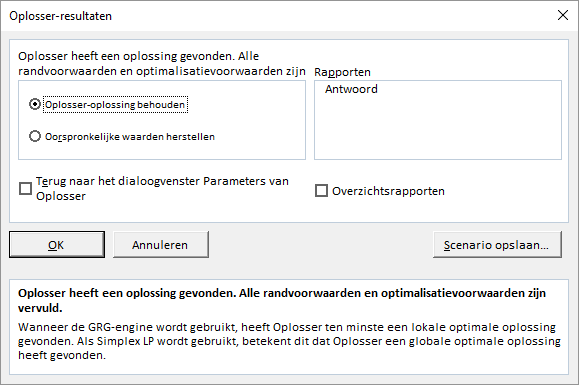
- Selecteer Oplossing behouden, selecteer Antwoord (vak Rapporten) en klik dan op OK.
Op het werkblad wordt nu het resultaat getoond dat door de Oplosser gevonden is.
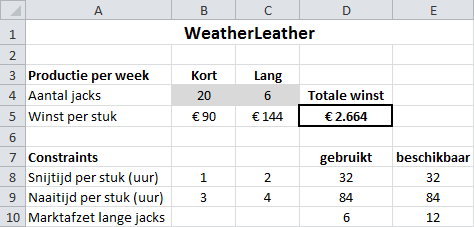
En er is ook een nieuw werkblad gemaakt met de naam Antwoordrapport ….
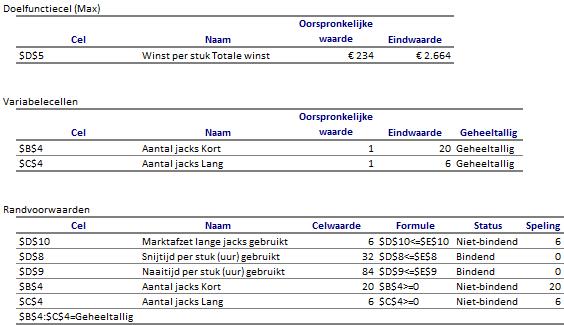
De vraag van WeatherLeather is nu opgelost. Er kan een maximale winst van € 2664 per week behaald worden door 20 korte jacks en 6 lange jacks per week te maken.
15.4 Geen oplossing gevonden. Wat nu?
Het komt regelmatig voor dat de Oplosser rapporteert dat geen oplossing gevonden kan worden:
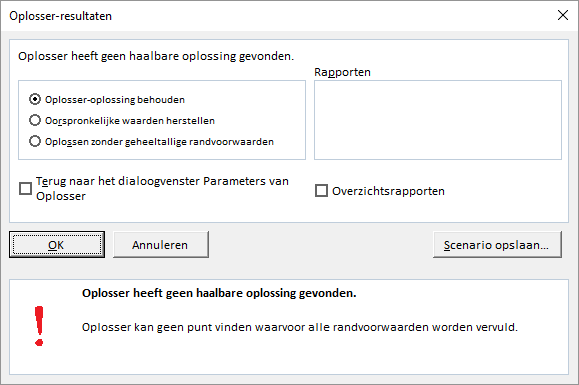
Er zijn nu twee mogelijkheden:
- Er bestaat geen oplossing voor het geformuleerde probleem.
- Er bestaat wel een oplossing voor het geformuleerde probleem, maar deze wordt niet door de Oplosser gevonden.
Je weet in de meeste gevallen nooit met zekerheid welke situatie aan de hand is. Er zijn wel een paar richtlijnen om te onderzoeken of er alsnog een oplossing door de Oplosser gevonden kan worden.
Wijziging beginwaarden veranderende cellen
Of de Oplosser een bestaande oplossing kan vinden hangt onder andere af van de beginwaarden voor de veranderende cellen. Door met andere beginwaarden te experimenteren kan uitgezocht worden of dan wel een oplossing gevonden kan worden.
Wijziging instellingen Oplosser
Het vinden van een oplossing hangt ook van de wijze waarop de Oplosser dit doet. Het zoeken naar een oplossing verloopt volgens een zogenaamd iteratief proces. Een iteratie is een herhaalde herberekening van het werkblad totdat aan een bepaalde voorwaarde is voldaan. De Oplosser kent een aantal instellingen voor dit iteratieproces. Door te klikken op de knop Opties in het dialoogvenster Parameters Oplosser verschijnt een venster waar je verschillende opties van de Oplosser kunt wijzigen.
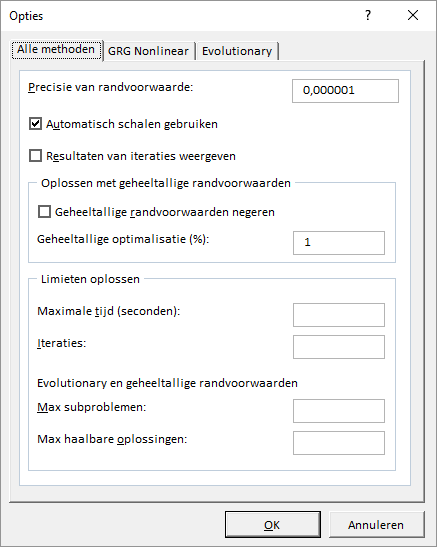
Het dialoogvenster biedt uitgebreide mogelijkheden om het oplosproces te besturen. En de specificaties voor bepaalde problemen kunnen als een model worden opgeslagen en weer geladen worden. Een paar van deze instellingen worden hier in het kort behandeld. Voor meer verdieping moet de literatuur bestudeerd worden.
| Instelling | Toelichting |
|---|---|
| Max tijd | Het maximaal aantal seconden die de Oplosser mag besteden aan het iteratieproces. De standaardwaarde van 100 sec. kan verhoogd worden wanneer de Oplosser rapporteert dat de toegestane tijd bereikt is. |
| Iteraties | Het maximaal aantal iteraties (herberekeningen). De standaardwaarde van 100 kan verhoogd worden wanneer geen oplossing gevonden kan worden. |
| Precisie | Hiermee wordt bepaald of de celwaarde van een restrictie aan de opgegeven voorwaarde voldoet. Hoe groter de precisie (meer decimalen)hoe langer het duurt voordat de Oplosser met resultaten komt. |
| Tolerantie | Het maximale foutpercentage dat is toegestaan bij integer oplossingen. De waarde is alleen van belang wanneer een restrictie met integer aanwezig is. Hoe kleiner het foutpercentage, hoe langer het zoekproces duurt. |
| Uitgaan van lineair model | Alleen gebruiken wanneer alle relaties in het berekeningsmodel lineair zijn. De keuze kan dan het zoekproces versnellen. Gebruik hiervan bij niet-lineaire modellen kan er juist voor zorgen dat er geen oplossing wordt gevonden. |
| Iteratieresultaat tonen | Bij inschakelen hiervan stopt de Oplosser na elke iteratie (herberekening)en geeft dan het resultaat weer. Normaliter niet gebruiken. |
| Precisie randvoorwaarde | Hiermee wordt bepaald of de celwaarde van een randvoorwaarde aan de opgegeven voorwaarde voldoet. Hoe groter de precisie (meer decimalen)hoe langer het duurt voordat de Oplosser met resultaten komt. |
| Maximale tijd | Het maximaal aantal seconden die de Oplosser mag besteden aan het iteratieproces. |
| Iteraties | Het maximaal aantal iteraties (herberekeningen). |
| Resultaten iteraties weergeven | Bij inschakelen hiervan stopt de Oplosser na elke iteratie (herberekening)en geeft dan het resultaat weer. Normaliter niet gebruiken. |
Aanvullende informatie:
Support site van Frontline Systems (Engelstalig), de ontwikkelaar van Oplosser.
15.5 Opgaven
Oefening 15.1 Bonbondoos (solv001)
Een bekende bonbonfabrikant wil een assortimentdoos uitbrengen met 2 soorten bonbons (kersenbonbons en hazelnootbonbons)en daarbij zoveel mogelijk winst behalen. Bekend is verder:
- Een kersenbonbon neemt 16 cm2 ruimte in en een hazelnootbonbon 8 cm2. De bonbons worden door papier van elkaar gescheiden. Minimaal 320 cm2 van de doos moet met bonbons bedekt zijn.
- Een kersenbonbon weegt 2 gram en een hazelnootbonbon weegt 1 gram. Uit marktonderzoek is gebleken dat het ideale gewicht van de inhoud van de doos tussen de 40 gram en 60 gram moet liggen.
- Ook is uit marktonderzoek gebleken dat de doos minstens 35 bonbons moet bevatten waarvan zeker 10 kersenbonbons.
- De winst op een kersenbonbon is 28 eurocent en op een hazelnootbonbon 20 eurocent.
- Wat zijn de beslissingsvariabelen?
- Wat is de doelfunctie?
- Welke restricties zijn er?
- Bouw het model in Excel en gebruik de in dit studieboek aangegeven richtlijnen. Een voorbeeld zie je in de volgende figuur. Beide beslissingsvariabelen hebben hierin als startwaarde 10 gekregen. Bij dit getal kun je gemakkelijk controleren of de formules de juiste uitkomsten geven.

- Bepaal met de Oplosser het optimale aantal bonbons per doos van elke soort.
- Twee beslissingsvariabelen:
- Aantal kersenbonbons per doos (= K)
- Aantal hazelnootbonbons per doos (= H)
- Doelfunctie is de maximale winst op een doos (= W):
W = 0,28*K + 0,20*H - Restricties:
- Aantal kersenbonbons per doos:
K >= 10 - Totaal aantal bonbons per doos:
K + H >= 35 - Gewicht doos:
2*K + 1*H >= 40 - Gewicht doos:
2*K +1*H <= 60 - Oppervlakte bonbons:
16*K + 8*H >= 320 - Aantal bonbons is een geheel getal:
K = integer , H = integer - Aantal bonbons is een positief getal:
K >= 0 , H >= 0
- Aantal kersenbonbons per doos:
Optimale inhoud doos: aantal kersenbonbons = 10, aantal hazelnootbonbons = 40. De winst per doos is dan € 10,80 en aan alle restricties wordt voldaan.
Oefening 15.2 Aantal supermarkten (solv002)
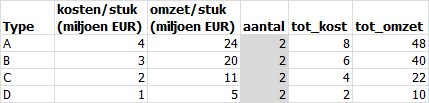
Een supermarktketen wil voor maximaal 14 miljoen euro een aantal nieuwe vestigingen openen. De keten heeft 4 soorten winkels, te weten van type A, B, C en D. De kosten voor het opzetten van de vier typen winkels en de (verwachte) omzet in het volgend boekjaar zijn in de volgende afbeelding te zien.
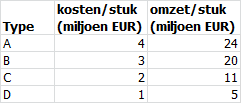
Alle nieuw te bouwen vestigingen kunnen voor het komende boekjaar gereed zijn. De eventuele vestigingsplaatsen zijn qua bevolking vergelijkbaar. De directie wenst een zo groot mogelijke omzet van de nieuwe vestigingen in het komende boekjaar. Bepaal met de oplosser hoeveel winkels van welk type gebouwd dienen te worden en wat de te verwachten totale omzet zal zijn.
- Wat zijn de beslissingsvariabelen?
- Wat is de doelfunctie?
- Welke restricties zijn er?
- Bouw het model in Excel en gebruik de in dit studieboek aangegeven richtlijnen. Een voorbeeld zie je in de volgende figuur. Alle beslissingsvariabelen hebben hierin als startwaarde 2 gekregen.
- Bepaal met de Oplosser het optimale het optimale aantal winkels van elke type.
- Vier beslissingsvariabelen: Aantal winkels type A (= A), type B (= B), type C (= C)en type D (= D).
- Doelfunctie is de totale omzet (= O):
O = 24*A + 20*B + 11*C + 5*D - Restricties:
- Maximale investering:
4*A + 3*B + 2*C + 1*D <= 14 - Elk aantal winkels is een geheel getal:
A = integer , B = integer , C = integer , D = integer - Elk aantal winkels is een positief getal:
A >= 0 , B >= 0 , C >= 0 , D >= 0
- Maximale investering:
Optimale aantal winkels type A = 0, aantal type B = 4, aantal type C = 1, aantal type D = 0. De totale omzet = 91 miljoen EUR.
Oefening 15.3 Hardloopschoenen (solv003)
Een bedrijf in Hongkong heeft zich toegelegd op het fabriceren van amerikaanse hardloopschoenen. Het bedrijf maakt drie modellen: Runner, Lady T, en Super A en wil hiermee zoveel mogelijk winst maken.
- Het vervaardigen van 1 paar Runner kost 0,31 uur, van 1 paar Lady T kost 0,20 uur en van 1 paar Super A kost 0,25 uur. In totaal kan per week niet meer dan 150 uur geproduceerd worden.
- De kapitaalinvestering bedraagt per paar Runner, Lady T, Super A respectievelijk € 16, € 12 en € 10. Er is per week € 8000 hiervoor beschikbaar.
- Vanwege de beperkte machinecapaciteit kan er per week hoogstens 300 paar Runner, 400 paar Lady T en 400 paar Super A geproduceerd worden.
- Op 1 paar Runner wordt een winst gemaakt van € 6 en de winst per paar Lady T is € 5 en per paar Super A bedraagt deze € 4.
Bereken met de oplosser de optimale productieaantallen en de maximale winst per week.
- Wat zijn de beslissingsvariabelen?
- Wat is de doelfunctie?
- Welke restricties zijn er?
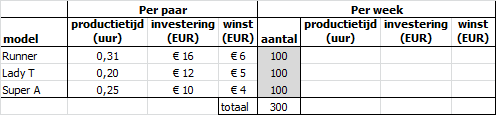
- Bouw het model in Excel en gebruik de in dit studieboek aangegeven richtlijnen. Een voorbeeld zie je in de volgende figuur. Beide beslissingsvariabelen hebben hierin als startwaarde 100 gekregen.
- Bepaal met de Oplosser het optimale aantal modellen en de maximale winst per week.
- Drie beslissingsvariabelen: Aantal model Runner per week (= R), aantal model Lady T per week (= T)en aantal model Super A per week (= A).
- Doelfunctie is de maximale winst per week (= W):
W = 6*R + 5*T + 4*A - Restricties:
- Aantal model Runner per week:
R <= 300 - Aantal model Lady T per week:
T <= 400 - Aantal model Super A per week:
A <= 400 - Maximale productietijd per week:
0,31*R 0,20*T + 0,25*A <= 150 - Maximale investering per week:
16*R + 12*T +10*A <= 8000 - Aantal van elk model is een geheel getal:
R = integer , T = integer , A = integer - Aantal van elk model is een positief getal:
R >= 0 , T >= 0 en A >= 0
- Aantal model Runner per week:
Optimaal aantal Runner = 111, aantal lady T = 400, aantal Super A = 142. De winst per week is € 3234.
Oefening 15.4 Productie aluminium ladders (solv004)
Een fabrikant van aluminium ladders maakt drie typen ladders. Om een ladder te maken moet eerst materiaal afgezaagd worden. Daarna vindt de assemblage plaats en tenslotte de afwerking. De productietijden alsmede de winst per ladder staan in de volgende tabel.
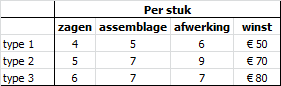
De totaal beschikbare productiecapaciteit is 80 voor zagen, 100 voor assemblage en 120 voor de afwerking.
Bepaal met behulp van de oplosser hoeveel ladders van elk type geproduceerd moeten worden opdat de winst maximaal is.
Aantal type 1 = 0, aantal type 2 = 4, aantal type 3 = 10, winst = € 1080.
Oefening 15.5 Productie hondenvoer (solv005)
Er zijn twee soorten hondevoer te koop: gewoon en speciaal. Een zak gewoon voer bevat 3 eenheden mineralen, 2 eenheden eiwit en 3 eenheden vet. Deze zak kost € 8. Een zak speciaal voer bevat 8 eenheden mineralen, 2 eenheden eiwit en 1 eenheid vet. De prijs van deze zak is € 14. Over een bepaalde periode moet de hond minstens 72 eenheden mineralen, 36 eenheden vet en 36 eenheden eiwit binnen krijgen.
Bepaal met behulp van de oplosser welke hoeveelheden van beide zakken gekocht moeten worden om de maaltijdkosten zo laag mogelijk te houden.
Aantal zakken gewoon = 14, aantal zakken speciaal = 4, maaltijdkosten = € 168.
Oefening 15.6 Vitamines in veevoer (solv006)
Een boer gebruikt drie typen veevoer, type 1, type 2 en type 3. De voedingssamenstelling en de kosten per kg van elk type is in de volgende afbeelding weergegeven.
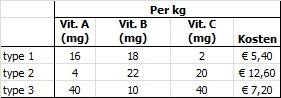
In een vaktijdschrift zijn de minimale dagbehoeftes (MDB)in milligram per dier voor de vitamines A, B en C gepubliceerd. Deze zijn 120 mg A, 180 mg B en 100 mg C. Verder kan een dier niet meer eten dan 7½ kg van type 1 en 5 kg van type 2 en 2½ kg van type 3.
Hoeveel kg van elk type moet de boer elke dag verstrekken om de kosten zo laag mogelijk te krijgen en toch te voldoen aan de minimale dagbehoefte?
Per dag: type 1 = 7,500 kg, type 2 = 1,397 kg, type 3 = 1,426 kg , kosten = € 68,37.
Oefening 15.7 Vitaminetabletten (solv007)
Een voedingsdeskundige beveelt een patient de volgende minimale dagbehoeftes vitamine B en C aan: 400 eenheden vitamine B en 800 eenheden vitamine C. De plaatselijke apotheek kan twee verschillende vitaminetabletten leveren, merk Y en merk Z. Een vitaminetablet van merk Y bevat 75 eenheden vitamine B en 100 eenheden vitamine C en kost € 0,10. Een vitaminetablet van merk Z bevat 50 eenheden vitamine B en 200 eenheden vitamine C en kost € 0,08. Hoeveel vitaminetabletten van elk soort moeten elke dag genuttigd worden tegen zo laag mogelijke kosten?
Per dag: aantal per merk Y = 4, aantal merk Z = 2, kosten = € 0,56.
Oefening 15.8 Transportkosten minimaliseren (solv008)
Bestand: Solv008.xlsx
Een bedrijf heeft winkels in 6 plaatsen (Amersfoort, Eindhoven, Enschede, Lelystad, Tiel, Zwolle). De bevoorrading van de winkels gebeurt vanuit drie distributiecentra (DC) in Coevorden, Venlo en Woerden. Wekelijks maken de winkels een afzetprognose voor de week erop en geven het benodigde aantal produkten door aan het hoofdkantoor. Op het hoofdkantoor maakt men aan de hand van de beschikbare voorraden in de DC’s een vervoersplanning om de winkels van het benodigde aantal produkten te voorzien.
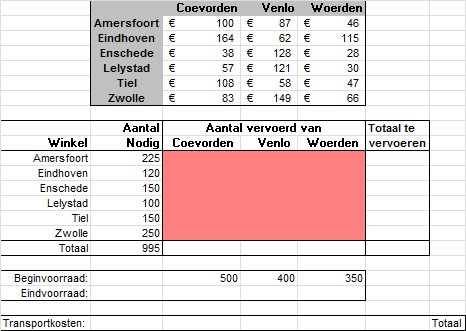
Toelichting:
- In de bovenste tabel staan de vervoerskosten in euro’s per eenheid product van het DC naar de winkel. Zo kost het vervoer van 1 product van het DC Coevorden naar de winkel in Amersfoort € 100.
- In de kolom “Aantal Nodig” staat het aantal producten dat de winkel moet ontvangen. Zo moet Amersfoort 225 producten ontvangen.
- In het gebied “Aantal vervoerd van” moet het aantal producten komen te staan dat van het desbetreffende DC naar de winkel vervoerd wordt. De Oplosser moet deze aantallen bepalen.
- De rij “Beginvoorraad” bevat het aantal producten dat op dit moment in het DC in voorraad is.
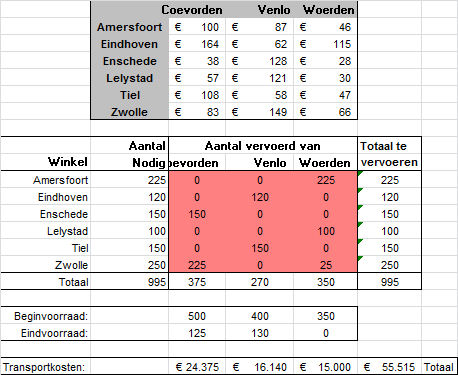
Maak met behulp van de oplosser een zodanige vervoersplanning te maken dat de kosten minimaal zijn.
Oefening 15.9 Stelsel lineaire vergelijkingen oplossen (solv009)
Los met behulp van de oplosser het volgende stelsel vergelijkingen op.
\[\begin{align*} 6,1x_1 + 4,5x_2 + 5,7x_4 + 7,5x_5 &= 5,7\\ 2,4x_1 + 5,5x_2 - 5,7x_3 + 4,7x_4 + 5,6x_5 &= 5,6\\ 2,4x_1 - 5,0x_2 - 4,6x_3 + 3,6x_4 + 9,7x_5 &= 9,7\\ 4,3x_1 - 5,3x_2 + 3,4x_3 - 8,4x_4 - 5,6x_5 &= -5,6\\ 1,1x_1 - 3,0x_2 + 2,4x_3 - 13x_4 + 3,5x_5 &= 3,5 \end{align*}\]
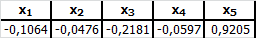
Oefening 15.10 Spaarbank (solv010)
Een spaarbank heeft 3 miljoen euro om te beleggen. De beleggingsportefeuilles zijn persoonlijke leningen, hypotheken (eerste en tweede hypotheken) en autoleasing. In de statuten van de bank staan een aantal voorwaarden t.a.v. de besteding van de gelden:
- Minimaal 30% van het totaal uitgeleende bedrag moet voor hypotheken bestemd zijn.
- Van het voor hypotheken bestemde bedrag moet minstens 50% voor eerste hypotheken aangewend worden.
- Maximaal 25% van het totaal uitgeleende bedrag mag aan persoonlijke leningen en autoleasing samen besteed worden.
- Maximaal 15% van het totaal uitgeleende bedrag mag aan persoonlijke leningen bestemd worden.
De jaarlijkse opbrengst van elk type lening is in de volgende tabel weergegeven.
| Type lening | Opbrengst |
|---|---|
| Persoonlijke lening | 18% |
| Eerste hypotheek | 12% |
| Tweede hypotheek | 14% |
| Autolease | 16% |
Bepaal met de oplosser hoeveel geld (in veelvouden van € 1000,-) voor elk van de vier typen leningen uitgegeven moet worden zodat de opbrengst zo hoog mogelijk wordt.
| Type lening | Bedrag |
|---|---|
| Persoonlijke lening | 450 K€ |
| Eerste hypotheek | 1125 K€ |
| Tweede hypotheek | 1125 K€ |
| Autolease | 300 K€ |
Totale opbrengst 422 K€. Bij weergave op eurocent nauwkeurig kunnen er afrondingsverschillen zijn.