17 Meetresultaten verwerken
Onderzoekers willen graag een antwoord hebben op de vraag of de waarde van een variabele afhangt van de waarde van een andere variabele. Om daar achter te komen voeren zij metingen uit. Bij het uitvoeren van de metingen wordt de waarde van één variabele steeds gewijzigd (de onafhankelijke variabele)en wordt de waarde van een andere variabele (de afhankelijke variabele) gemeten.
Deze metingen leveren een serie meetwaarden op die in een grafiek kunnen worden uitgezet. Het verloop van de grafiek geeft vaak al een eerste indruk of er een relatie is tussen de twee variabelen en zoja welk soort relatie: lineair, exponentieel, logaritmisch, …
Een relatie tussen variabelen wordt weergegeven door een wiskundige functie en aangeduid met een vergelijking. Wanneer de relatie lineair is, is de grafiek een rechte lijn.
Bij het grafisch weergeven van meetresultaten zal er bijna nooit een lijn zijn die precies past bij alle meetpunten. Met behulp van statistische technieken zijn programma’s als Excel in staat om de best passende lijn bij deze meetpunten te bepalen. Zo’n lijn wordt ook wel regressielijn genoemd. De rekenmethode om de best passende lijn te vinden staat bekend als de kleinste kwadratenmethode.
In het (gratis) online studieboek Data Analyse met Excel wordt meer aandacht besteed aan de achtergronden van deze methode en de verschillende trendlijnen die je met Excel kunt maken
17.1 Lineair verband
Wanneer tussen twee variabelen \(x\) en \(y\) een lineair verband bestaat dan kan de relatie tussen deze twee variabelen worden weergegeven met de vergelijking
\(y = ax + b\)
- \(y\) is de afhankelijke variabele
- \(x\) is de onafhankelijke variabele
- \(a\) is de richtingscoëfficiënt, een constante
- \(b\) is het snijpunt met de y-as, een constante
Voorbeeld 17.1 \(y = 2x + 3\)
De grafiek van \(y=2x+3\) is een rechte lijn. De richtingscoëfficiënt van de lijn, \(a\), is 2, en het snijpunt met de y-as, \(b\), is 3.
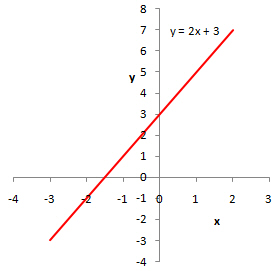
Wanneer een aantal meetresultaten bekend zijn, dan kun je met Excel
- een grafiek tekenen.
- de trendlijn tekenen (de best passende lijn).
- de vergelijking van de trendlijn bepalen.
- de richtingscoeëfficiënt en het snijpunt met de y-as bepalen met Excel functies.
17.2 Lineaire trendlijn
In een houtfabriek wordt een groot aantal gelijksoortige artikelen gefabriceerd, die hoofdzakelijk verschillen vertonen in hun afmetingen en gewicht. Om te onderzoeken of de productietijd van deze artikelen afhangt van het gewicht ervan, worden een aantal metingen uitgevoerd. Er wordt een linair verband verondersteld.
Taak 17.1 Bestand: Productietijd_Gewicht.xlsx
Open het bestand.
Selecteer het gebied met de meetresultaten, A2:B11.
Kies tab Invoegen > Aanbevolen grafieken (groep Grafieken) > Spreiding > OK.
Voeg een lineaire trendlijn toe.
Je kunt op de volgende manieren een trendlijn toevoegen.
- Selecteer de punten in de grafiek, dan rechter muisklik en kies Trendlijn toevoegen.
- Selecteer het grafiekgebied en klik op de knop
naast de grafiek en kies Trendlijn > Lineair.
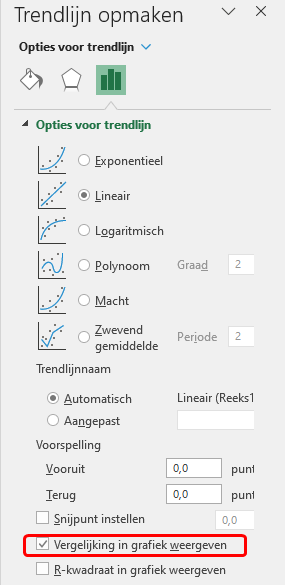
Selecteer trendlijn, Rechter muisklik > Trendlijn opmaken.
Selecteer in het taakvenster Trendlijn opmaken de optie Vergelijking in grafiek weergeven.
Maak de volgende aanpassingen (zie het voorbeeld in Figuur 17.3):
- Voeg grafiektitel en astitels toe.
- Pas de schaling van de assen aan.
- Geen decimalen in de getallen langs de assen.
- Maak van de trendlijn een getrokken rode lijn.
- Versleep de vergelijking naar een beter zichtbare plek.
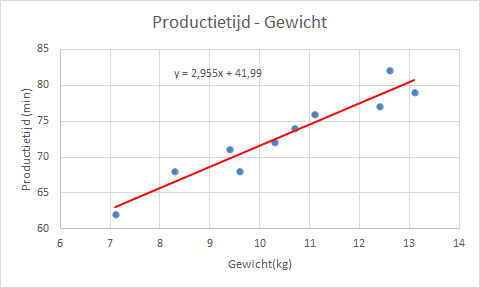
Uit de vergelijking van de trendlijn kan nu het lineaire verband tussen de twee variabelen worden afgelezen:
\(\text{Productietijd} = 2,955 \times \text{Gewicht} + 41,99\)
Werkbladfuncties
De richtingscoëfficiënt van de trendlijn en het snijpunt met de y-as kunnen ook berekend worden met de functies RICHTING en SNIJPUNT uit de categorie Statistisch.
Selecteer een lege cel op het werkblad en voer de functie
RICHTINGin. Specificeer hierbij- y-bekend: B2:B11
- x-bekend: A2:A11
Bepaal op dezelfde manier in een andere cel de waarde van
SNIJPUNT.
De waarde van de richtingscoëfficient: 2,95503212 en de waarde van snijpunt is 41,99036403. Hiermee zijn de gegevens voor de vergelijking van de trendlijn bekend.
17.3 Opgaven
Oefening 17.1 Lengte en gewicht (meas001)
Van een aantal schoolkinderen zijn lengte en gewicht bepaald. In de figuur hierna staan de meetresultaten.
Veronderstel een lineair verband en bepaal de vergelijking waarbij het gewicht een functie is van de lengte.
Bestand: Meas001.xlsx
Gewicht = 1,65*Lengte - 153,3
Oefening 17.2 Studietijd en tentamencijfer (meas002)
Van een zestal studenten is het aantal studie-uren bijgehouden dat zij aan een bepaald vak hebben besteed en verder het tentamencijfer dat voor dat vak behaald is. In de figuur hierna staan de resultaten.
Veronderstel een lineair verband en bepaal de vergelijking waarbij het cijfer verklaard kan worden uit de studietijd.
Bestand: Meas002.xlsx
Cijfer = 0,2038*Studietijd + 3,3637
Oefening 17.3 Krimp en temperatuur (meas003)
Een fabrikant van synthetische vezels onderzoekt of het krimpen van de vezels samenhangt met de temperatuur waarbij ze gewassen worden. Er worden 8 experimenten uitgevoerd waarbij de vezels bij verschillende temperaturen worden gewassen. De gemeten krimp is hierna weergegeven in procenten van de oorspronkelijke lengte.
- Veronderstel een lineair verband en bepaal de vergelijking waarbij het krimppercentage verklaard kan worden uit de temperatuur.
- Voorspel met behulp hiervan de krimp bij een temperatuur van 65oC.
Bestand: Meas003.xlsx
Krimpperc = 0,0796*Temp - 3,546
Bij een temperatuur van 65oC is het voorspelde krimppercentage 1,6%.
Oefening 17.4 Weerstand en temperatuur (meas004)
De weerstand van een metalen blokje hangt o.a. af van de temperatuur. In de afbeelding hierna is de de gemeten weerstand te zien bij een zevental temperaturen.
- Veronderstel een lineair verband en bepaal de vergelijking waarbij de weerstand verklaard kan worden uit de temperatuur.
- Voorspel met behulp hiervan de weerstand van het blokje bij een temperatuur van 400oC.
Bestand: Meas004.xlsx
Weerstand = 0,0786*Temp + 21,214
Bij een temperatuur van 400oC is de voorspelde weerstand 52,6 Ohm.