8  Matrixformules

Doelstellingen

  • Kennismaking met een matrix.
  • Het maken van matrixformules.
  • Frequentieverdeling van gegevens maken met functie iNTERVAL.
  • Dynamische matrices en bijbehorende functies.
  • Wiskundige matrixfuncties.

Een matrixformule is een formule die meerdere berekeningen kan uitvoeren op een of meer items in een matrix. Matrixformules stonden als erg lastig bekend omdat ze er anders uitzien dan normale formules en je deze formules op een afwijkende manier moest invoeren: met CTRL-SHIFT-ENTER in plaats van gewoon met ENTER. Dat is in Excel 365 niet langer nodig.

  1. In Excel 365 is het werken met matrixformules en het gedrag ervan gewijzigd t.o.v. de andere Excel versies. En ook bestaande formules die meerdere resultaten kunnen opleveren gedragen zich in Excel 365 als matrixformules.

  2. Aan Excel 365 zijn een aantal nieuwe dynamische matrixformules toegevoegd.

Hierdoor is de inhoud van dit hoofdstuk grotendeels exclusief voor Excel 365.

8.1 Wat is een matrix in Excel?

Een vector is een lijstje met getallen die of in een rij of in een kolom staan. Je hebt dan respectievelijke een rijvector of een kolomvector. Excel gebruikt niet de term vector, maar matrix (Nederlandstalig )of array (Engelstalig).

Een matrix in Excel kan zijn:

  • Een rij met waarden (eigenlijk een rijvector). Dit is een 1-dimensionale horizontale matrix.
  • Een kolom met waarden (eigenlijk een kolomvector). Dit is een 1-dimensionale verticale matrix.
  • Een rechthoek van rijen en kolommen met waarden, een gebied dus. Dit is een 2-dimensionale matrix.

Figuur 8.1 laat van elk een voorbeeld zien.

Figuur 8.1: Matrix voorbeelden, met van links naar rechts: rijvector, kolomvector, 2-dim. matrix.

Een matrix met constante waarden zoals in de getoonde drie voorbeelden maak je door in een cel te beginnen met het = symbool en dan een rijtje waarden tussen accolades { } te plaatsen. De waarden moeten van elkaar gescheiden worden door een speciaal symbool.Het scheidingssymbool hangt af van de taal- en landinstellingen op de computer.

  • Nederlandstalige systemen
    • Backslash \ voor nieuwe kolom.
    • Puntkomma ; voor nieuwe rij.
  • Engelstalige systemen
    • Komma , voor nieuwe kolom.
    • Puntkomma ; voor nieuwe rij.

Verder moet je bij een 2-dimensionale matrix rekening houden met:

  • Opsomming in volgorde van rijen.
  • Alle rijen moeten evenveel kolommen hebben.

De drie voorbeelden worden als volgt in Excel ingevoerd.

Voorbeeld 8.1 Rijvector

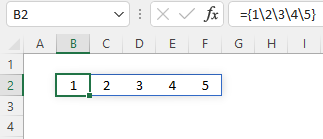
={1\2\3\4\5} geeft 1 rij met 5 kolommen.

Figuur 8.2: 1-dimensionale horizontale matrix.

Voorbeeld 8.2 Kolomvector

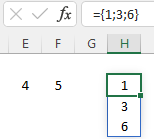
={1;3;6} geeft 3 rijen met 1 kolom.

Figuur 8.3: 1-dimensionale verticale matrix.

Voorbeeld 8.3 2-dimensionale matrix

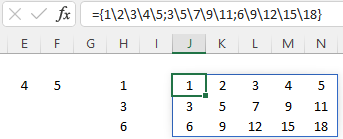
={1\2\3\4\5;3\5\7\9\11;6\9\12\15\18} geeft 3 rijen met 5 kolommen.

Figuur 8.4: 2-dimensionale matrix.

Voor alle voorbeelden geldt dat alleen de eerste cel bewerkbaar is. Dat is de cel waar de matrix is ingevoerd. Wanneer je een andere cel in het waardengebied selecteert, dan is de inhoud in de formulebalk grijs gekleurd en kun je de waarde niet wijzigen.

8.2 Eenvoudige matrixformules

Een matrixformule is een formule waarmee je berekeningen uitvoert op matrices. Het resultaat is ook weer een matrix. Om matrixformules te gebruiken moet je van tevoren bedenken hoeveel uitkomsten er zijn en hoe deze uitkomsten zijn gerangschikt (een cel, een rij, een kolom, een tabel).

In Figuur 8.5 is te zien dat een paar keer de som en het produkt van twee getallen is berekend. Dat kan met eenvoudige gewone formules. Zo zou de formule in D2 kunnen zijn =A2+B2. En de formule in E2 zou kunnen zijn =A2*B2. Wanneer je dan deze formules naar beneden kopieert dan staan de juiste formules ook in D3:E4.

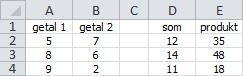
Figuur 8.5: Som en product van twee getallen via gewone Excel formules.

Deze berekening is ook met matrixformules uit te voeren. Het is een goede oefening om het gedrag van een matrixformule te leren kennen.

Taak 8.1 Bestand: Matrix1.xlsx

  1. Open het bestand.

  2. Selecteer cel D2 en typ in =A2:A4+B2:B4 en druk op ENTER.
    De resultaten staan in de cellen D2:D4 en aan het kader om het resultaat kun je zien dat het een matrix is.

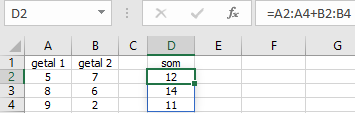
Figuur 8.6: Som van twee kolommen via een matrixformule.

  • In plaats van het intypen van de celadressen kun je deze ook met de muis selecteren, wat veel handiger is.

  • Omdat het resultaat van de optelling uit een kolommetje van drie getallen bestaat zal Excel het resultaat automatisch laten overlopen naar de cellen D3:D4. Je moet dat wel vooraf bedenken en zorgen dat deze cellen leeg zijn, anders volgt de foutmelding #OVERLOOP!.

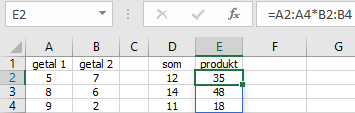
  1. Selecteer cel E2 en typ in =A2:A4*B2:B4 en druk nu op ENTER.
    De resultaten staan in de cellen E2:E4 en aan het kader om het resultaat kun je zien dat het een matrix is.
Figuur 8.7: Product van twee kolommen via een matrixformule.

Taak 8.2 Vermenigvuldiging rijvector met een getal

In Figuur 8.8) is te zien hoe een rijtje van drie getallen wordt vermenigvuldigd met het getal 4. Het resultaat bestaat uit een rijtje van drie getallen. Maak dit voorbeeld na.

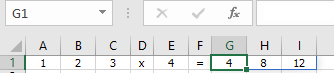
Figuur 8.8: Vermenigvuldiging rijvector met een constante.

Formule in G1: =A1:C1*E1

Taak 8.3 Vermenigvuldiging 2-dim matrix met een kolomvector

In Figuur 8.9 is te zien hoe een 4x3 matrix wordt vermenigvuldigd met een kolom getallen. Het resultaat is ook weer een 4x3 matrix.

Maak dit voorbeeld na. Hierbij kun je gebruik maken van het bestand Matrix2.xlsx.

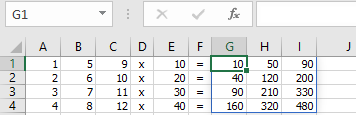
Figuur 8.9: Vermenigvuldiging van een 2-dimensionale matrix met een kolomvector.

Formule in G1 wordt A1:C4*E1:E4

8.3 Eén resultaat berekenen

In dit onderdeel wordt uitgelegd hoe je één matrixformule kunt gebruiken in situaties waar je anders meerdere formules voor nodig hebt.

Je kunt een matrixformule gebruiken wanneer je diverse berekeningen moet uitvoeren om één resultaat te krijgen. Dit type matrixformule kan een werkblad vereenvoudigen doordat meerdere formules worden vervangen door één matrixformule.

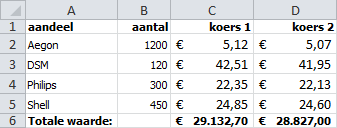
In Figuur 8.10 is een aandelenportefeuille met koersen te zien. Om nu de totale waarde van de aandelen bij een bepaalde koers te berekenen zou je normaliter voor elk aandeel de waarde moeten berekenen via aantal * koers en dan deze waarden optellen. Met een matrixformule kan dit resultaat in één keer berekend worden.

Figuur 8.10: Koersen van aandelen.

Taak 8.4 Bestand: Matrix3.xlsx

  1. Open het bestand.

  2. Selecteer cel C6 en voer de volgende formule in =SOM(B2:B5*C2:C5).

  3. Herhaal de actie voor cel D6, de formule wordt nu =SOM(B2:B5*D2:D5).

Vraag

Je kunt de formule in C6 ook geschikt maken om naar D6 te kopieren. Wat moet je daarvoor in de formule veranderen?

De celadressen voor aantal]{.varname} moet je dan absoluut maken. De formule wordt [=SOM($B$2:$B$5*C2:C5).

Taak 8.5 Bestand: Matrix4.xlsx

In deze oefening moet voor elke leerling het gewogen gemiddelde van vier toetsen berekend worden met een matrixformule berekend. Begin met een formule voor Jan en maak deze formule geschikt om naar beneden te kopieren.

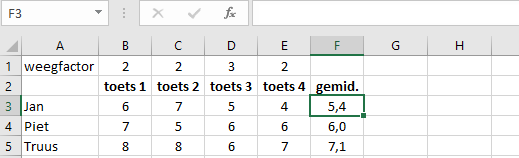
Figuur 8.11: Gewogen gemiddeldes van behaalde cijfers voor vier toetsen.

  1. Een gewogen gemiddelde voor Jan krijg je door elk toetscijfer van Jan te vermenigvuldigen met de weegfactor voor die toets en dan de som van deze vier uitkomsten te delen door de som van de vier toetsfactoren.

  2. Om de formule geschikt te maken om gekopieerd te kunnen worden, moet je nadenken over welke celadressen tijdens het kopieren niet mogen wijzigen. Die celadressen moet je dan absoluut maken.

Formule F3: =SOM(B3:E3*$B$1:$E$1)/SOM($B$1:$E$1)

Kopieer daarna formule naar F4 en F5.

Taak 8.6 Bestand: Matrix5.xlsx

In Figuur 8.12 is van een aantal studenten het geslacht en de lengte (cm) vermeld. In de cellen C11 en C12 is de gemiddelde lengte voor respectievelijk de mannelijke en vrouwelijke studenten berekend.

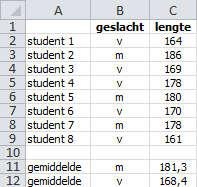
Figuur 8.12: Gemiddelde lengte van studenten per geslacht.

De matrixformule in deze oefening is wat lastiger omdat je alleen de lengtes voor of man of vrouw moet selecteren. Dat kan met de ALS functie.

  1. Open het bestand.

  2. Selecteer cel C11 en voer de volgende formule in =GEMIDDELDE(ALS(B2:B9="m";C2:C9)).

  3. Maak nu een formule voor cel C12 door de formule hiervoor aan te passen voor de vrouwelijke studenten.

Formule C12: =GEMIDDELDE(ALS(B2:B9="v";C2:C9))

8.4 Frequentieverdeling

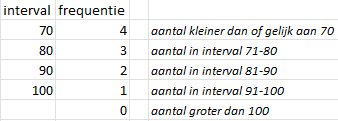
Met de functie INTERVAL() kun je een frequentieverdeling maken.

Syntax: INTERVAL(gegevensmatrix;interval).

Het eerste argument is het gebied met waarden. Het tweede argument is het gebied met de intervalgrenzen. Het resultaat is een matrix met de frequenties.

Taak 8.7 Bestand: Matrix6.xlsx

Figuur 8.13: Frequentieverdeling.

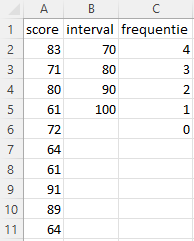
  1. Open het bestand.

  2. Voer in C2 de volgende formule in =INTERVAL(A2:A11;B2:B5).

Het resultaat is een frequentietabel. In de figuur hierna kun je zien hoe de frequenties bepaald zijn.

8.5 Dynamische matrixformules

Een matrixformule die in één cel op het werkblad wordt ingevoerd kan resultaten in meerdere cellen op het werkblad plaatsen. Dit gedrag wordt overlopen (Engels: spilling) genoemd en de resultaten verschijnen in een overloopgebied (spill-range). Welke en hoeveel cellen gebruikt worden hangt van het resultaat van de formule af. Als de broninhoud van de formule verandert worden de resultaten dynamisch bijgewerkt en kan het zijn dat het overloopgebied groeit of krimpt. Je krijgt een #OVERLOOP!fout wanneer het overlopen geblokkeerd wordt door andere gegevens in de cellen.

Om een verwijzing naar een overloopgebied te maken zet je een hash symbool # achter het adres van de eerste cel van het overloopgebied. Is bijvoorbeeld het overloopgebied J2:N4, dan verwijs je hiernaar met =J2#. Wanneer later de grootte van het overloopgebied verandert, dan verandert ook het resultaat van de formule.

Wanneer je met matrices gaat rekenen, is het erg handig om deze van een naam te voorzien. Dat kan op dezelfde manier als het toekennen van een naam aan een cel.

Om het gedrag van dynamische arrays te ondersteunen, zijn er een aantal nieuwe functies vrijgegeven: RANDARRAY, FILTER, SEQUENCE, SORT, SORTBY, UNIQUE, XMATCH en XLOOKUP.

8.5.1 ASELECT.MATRIX

Engelstalige functienaam: RANDARRAY

Retourneert een matrix met willekeurige getallen.

Syntax

ASELECT.MATRIX([rijen];[kolommen];[min];[max];[geheel])

  • rijen: het aantal rijen dat geretourneerd moet worden (default=1)
  • kolommen: het aantal kolommen dat moet worden (default=1)
  • min: de ondergrens van de willekeurige getallen (default=0)
  • max: de bovengrens van de willekeurige getallen (default=1)
  • geheel: WAAR voor gehele getallen, ONWAAR voor decimale getallen (default ONWAAR)

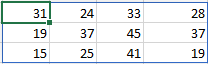
Voorbeeld 8.4 =ASELECT.MATRIX(3;4;10;50;WAAR)

Figuur 8.14: Genereert een 3x4 matrix met willekeurige gehele getallen tussen 10 en 50.

8.5.2 FILTER

Engelstalige functienaam: FILTER

Retourneert de gefilterde waarden uit een bereik/matrix.

Syntax

FILTER(matrix;opnemen;[als-leeg])

  • matrix: de matrix met waarden
  • opnemen: matrix met logische waarden voor de voorwaarden
  • als-leeg: te retourneren waarde wanneer er geen resultaten zijn

Voorbeeld 8.5 Bestand: Dynarray.xlsx

Extraheer de rijen met geslacht vrouwelijk.

=FILTER(A2:C11;B2:B11="v";"Geen")

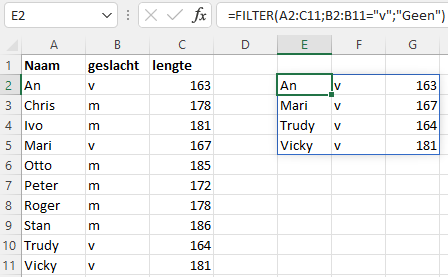
Figuur 8.15: Uit een lijst met namen worden die rijen gehaald waarvoor het geslacht vrouwelijk is.

Vervang in de formule de “v” eens door “m” of “z”.

Je kunt ook meerdere criteria toevoegen. Om te filteren op vrouwen met een lengte kleiner dan 170 wijzig je de formule in
=FILTER(A2:C11;(B2:B11="v")*(C2:C11<170);"Geen")

8.5.3 REEKS

Engelstalige functienaam: SEQUENCE

Retourneert een reeks getallen volgens een patroon.

Syntax

REEKS(rijen;[kolommen];[beginnen];[stap])

  • rijen: het aantal rijen dat geretourneerd moet worden
  • kolommen: het aantal kolommen dat geretourneerd moet worden (default=1)
  • beginnen: het eerste getal (default=1)
  • stap: de stapgrootte (default=1)

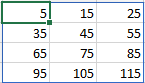
Voorbeeld 8.6 =REEKS(4;3;5;10)

Figuur 8.16: Genereert een 4x3 matrix met gehele getallen, beginnend met 5 en steeds 10 groter.

8.5.4 SORTEREN

Engelstalige functienaam: SORT

Sorteert de kolomwaarden uit een bereik/matrix.

Syntax

SORTEREN(matrix;[sorteerindex];[sorteervolgorde];[op-kol])

  • matrix: de matrix met waarden
  • sorteerindex: kolomindex waarop gesorteerd moet worden (default=1)
  • sorteervolgorde: de gewenste sorteervolgorde, 1= oplopend, -1 = aflopend (default=1)
  • op-kol: WAAR=sorteer kolommen, ONWAAR=sorteer rijen (default=ONWAAR)

Voorbeeld 8.7 Bestand: Dynarray.xlsx

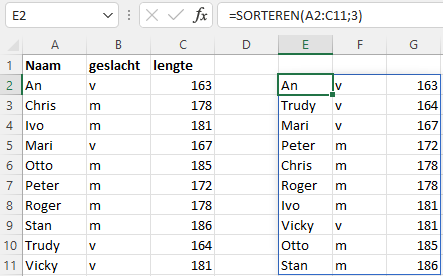
Een matrix met gegevens sorteren op de waarden in kolom 3.

=SORTEREN(A2:C11;3)

Figuur 8.17: Een matrix wordt gesorteerd op lengte (= kolom 3).

8.5.5 SORTEREN.OP

Engelstalige functienaam: SORTBY

Sorteert de waarden uit een bereik/matrix op basis van andere waarden.

Syntax

SORTEREN.OP(matrix;op-matrix1;[sorteervolgorde]; ...)

  • matrix: de matrix met waarden
  • op-matrix: de matrix waarop sortering gebaseerd moet worden
  • sorteervolgorde: 1= oplopend (default), -1 = aflopend

Voorbeeld 8.8 Bestand: Dynarray.xlsx

Namen sorteren op basis van lengte.

=SORTEREN.OP(A2:A11;C2:C11)

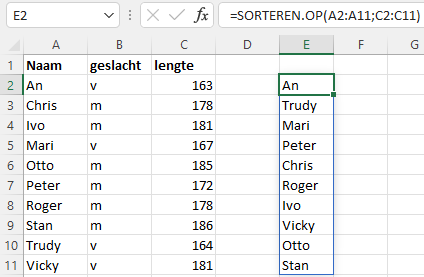
Figuur 8.18: Een lijst met namen wordt gesorteerd op lengte.

Zoals je ziet hoeft de reeks waarop de sortering berust niet in de uitvoer voor te komen.

Een andere toepassing van deze functie is bij het sorteren op twee kolommen.

Voorbeeld 8.9 Bestand: Dynarray.xlsx

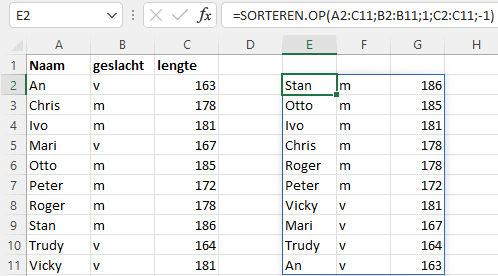
Sorteer de matrix oplopend op basis van geslacht en vervolgens aflopend op lengte.

=SORTEREN.OP(A2:C11;B2:B11;1;C2:C11;-1)

Figuur 8.19: Een matrix wordt oplopend gesorteerd op geslacht en vervolgens aflopend op lengte.

8.5.6 UNIEK

Engelstalige functienaam: UNIQUE

Retourneert een matrix met de unieke waarden uit een bereik/matrix.

Syntax

UNIEK(matrix;[per-kolom];[exact-eenmaal])

  • matrix: de matrix met waarden
  • per-kolom: WAAR (vergelijking van kolommen, ONWAAR (vergelijking van rijen, default)
  • exact-eenmaal: WAAR (retourneert de unieke waarden die precies één keer voorkomen), ONWAAR (retourneert alle unieke waarden, default)

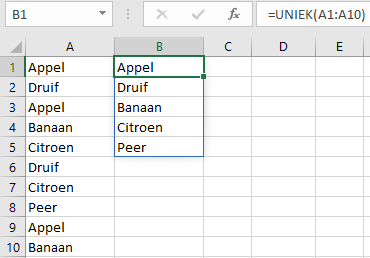
Voorbeeld 8.10 UNIEK(A1:A10)

Uit een reeks namen worden de unieke waarden gehaald.

Figuur 8.20: Uit een lijst met fruitnamen zijn de unieke waarden gehaald en in een nieuwe matrix geplaatst.

8.5.7 X.VERGELIJKEN

Engelstalige functienaam: XMATCH

De functie voert een zoekactie uit en retourneert een positie in verticale of horizontale bereiken. Het is een moderne en uitgebreidere opvolger van de functie VERGELIJKEN en wordt meestal gebruikt in combinatie met andere functies.

X.VERGELIJKEN ondersteunt benaderende en exacte overeenkomsten, omgekeerd zoeken en jokertekens (*?) voor gedeeltelijke overeenkomsten. Het opzoeken van de gegevens kan beginnen bij de eerste waarde of bij de laatste waarde (omgekeerd zoeken). Daarnaast kunnen ook binaire zoekopdrachten uitgevoerd worden.

Syntax

X.VERGELIJKEN(zoekwaarde;zoeken-matrix;[overeenkomstmodus];[zoekmodus])

  • zoekwaarde: de op te zoeken waarde
  • zoeken-matrix: de matrix waarbinnen gezocht moet worden
  • overeenkomstmodus: 0=exacte vergelijking (default), -1=exacte vergelijking of eerst kleinere, 1=exacte vergelijking of eerst grotere, 2=vergelijking met jokers
  • zoekmodus: 1=zoeken vanaf eerste (default), -1=vanaf laatste, 2=binair oplopend, -2=binair aflopend

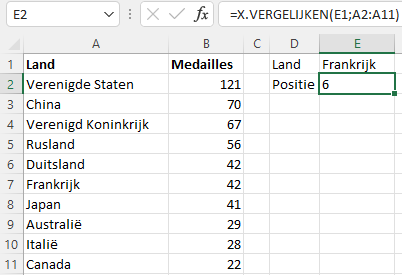
Voorbeeld 8.11 =X.VERGELIJKEN(E1;A2:A11)

Top 10 van het totaal aantal medailles op de Olympische Zomerspelen 2016.

Figuur 8.21: De positie van het land in cel E1 wordt bepaald.

8.5.8 X.ZOEKEN

Engelstalige functienaam: XLOOKUP

Deze functie is een moderne en uitgebreidere vervanging van oudere functies als VERT.ZOEKEN, HORIZ.ZOEKEN en ZOEKEN. Deze flexibele en krachtige functie ondersteunt benaderende en exacte overeenkomsten, jokertekens (*?) voor gedeeltelijke overeenkomsten en zoekmogelijkheden in verticale en horizontale bereiken.

Syntax

X.ZOEKEN(zoekwaarde; zoeken-matrix; matrix-retourneren; [indien-niet-gevonden]; [overeenkomstmodus]; [zoekmodus])

  • zoekwaarde: de op te zoeken waarde
  • zoeken-matrix: de matrix waarbinnen gezocht moet worden
  • matrix-retourneren: de matrix die geretourneerd moet worden
  • indien-niet-gevonden: waarde die geretourneerd moet worden wanneer er niets gevonden is
  • overeenkomstmodus: 0=exacte vergelijking (default), -1=exacte vergelijking of eerst kleinere, 1=exacte vergelijking of eerst grotere, 2=vergelijking met jokers
  • zoekmodus: 1=zoeken vanaf eerste (default), -1=vanaf laatste, 2=binair oplopend, -2=binair aflopend

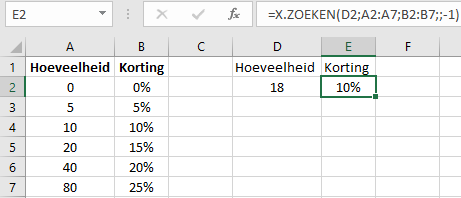
Voorbeeld 8.12 =X.ZOEKEN(D2;A2:A7;B2:B7;;-1)

Een kortingstabel met daarin de kortingspercentages vanaf een bepaalde hoeveelheid.

Figuur 8.22: Bepaling van het kortingspercentage voor de afnamehoeveelheid in cel D2.

Let goed op de argumenten in deze formule.

  • zoekwaarde: D2
  • zoeken-matrix: A2:A7
  • matrix-retourneren: B2:B7
  • indien-niet-gevonden: is niet gespecificeerd, vandaar dat er direct weer een puntkomma volgt.
  • overeenkomstmodus: -1
  • zoekmodus: is niet gespecificeerd, de defaultwaarde wordt dan gebruikt.

8.6 Tabellen en matrixformules

Matrixformules worden in de meeste gevallen gebruikt om acties uit te voeren op een lijst met gegevens, veelal in meerdere kolommen. Het heeft dan veel voordelen om van die gegevenslijst een echte Excel tabel te maken. In de matrixformules kun je dan voor de verwijzingen de tabel- en kolomnaam gebruiken en die daardoor beter leesbaar worden. Een bijkomend voordeel is dat de verwijzingen in orde blijven wanneer er tabelrijen worden toegevoegd of verwijderd.

Voor het verwijzen naar een kolomnaam in een Exceltabel zet je de kolomnaam tussen blokhaken direct achter de tabelnaam, dus tabelnaam[kolomnaam].

Taak 8.8 Bestand: Personeel.xlsx

  1. Open het bestand.

  2. Zet het gegevensbereik om naar een tabel via tab Invoegen > Tabel en specificeer tblPersoneel als tabelnaam.

  3. Sla het bestand tussentijds op onder de naam [Personeelstabel.xlsx` zodat het oorspronkelijke bestand niet gewijzigd wordt.

  4. Voer in een cel buiten het gegevensgebied, bijv. in cel K4, de volgende formule in =UNIEK(tblPersoneel[Afdeling]).

Je krijgt nu een lijst met de namen van de afdelingen. Om hiervan een alfabetisch gesorteerde lijst te maken moet je deze formule opnemen binnen de functie SORTEREN.

  1. Wijzig de zojuist ingevoerde formule in =SORTEREN(UNIEK(tblPersoneel[Afdeling])).

Je krijgt nu een alfabetisch gesorteerde lijst met afdelingsnamen.

Maak op analoge wijze een gesorteerde lijst met divisienamen.

8.7 Meerdere waarden retourneren

X.ZOEKEN kan meer dan één waarde tegelijk retourneren voor dezelfde overeenkomst. In deze taak worden vier waarden geretourneerd met één formule.

Taak 8.9 Bestand: olympic2016.xlsx

  1. Open het bestand.

  2. Zet het gegevensbereik om naar een tabel via tab Invoegen > Tabel en specificeer Medailles als tabelnaam.

  3. Voeg aan de tabel een kolom Totaal toe met daarin een formule voor het totaal aantal medailles. Dit gaat als volgt:

    • Typ in cel E1 de tekst Totaal en druk op ENTER. Er wordt nu automatisch een nieuwe kolom gemaakt.

    • Selecteer cel E2 en typ =SOM(]{.userinput}, selecteer dan de cellen B2:D2, typ dan [) en druk op ENTER.

In de kolom Totaal verschijnen nu de waarden. Merk verder op dat Excel in cel E2 de formule heeft gewijzigd in =SOM(Medailles[@[Goud]:[Brons]]).

  1. Kopieer de teksten in A1:E1 naar G1:K1.

  2. Typ in cel G2 de tekst Nederland.

  3. Selecteer H2 en typ in
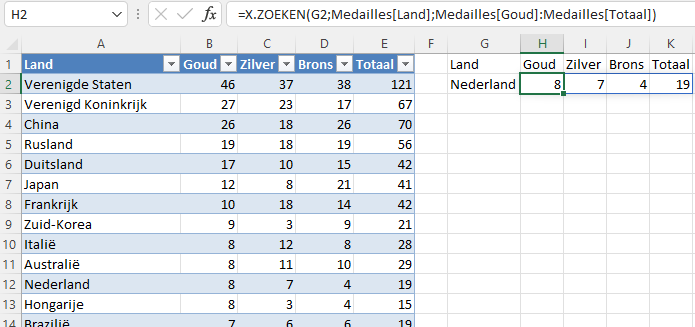
    =X.ZOEKEN(G2;Medailles[Land];Medailles[Goud]:Medailles[Totaal]).

Het resultaat ziet er als volgt uit.

Figuur 8.23: De formule in H2 retourneert meerdere waarden.

8.8 Opzoeken in twee richtingen

X.ZOEKEN kan ook ingezet worden om in twee richtingen te zoeken. Dat kan door een X.ZOEKEN functie op te nemen (nesten) binnen een andere X.ZOEKEN functie.

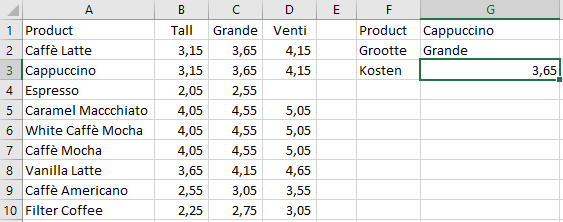
In Figuur 8.24 staan een aantal koffieprijzen van Starbucks. Aan de hand van zoekcriteria in G1 en G2 moet de bijbehorende prijs in G3 verschijnen.

Figuur 8.24: Geneste X.ZOEKEN functies.

Taak 8.10 Bestand: Tidy001.xlsx

  1. Open het bestand.

  2. Voeg de gegevens in F1:F3 en G1:G2 toe.

  3. Plaats in G3 de volgende formule
    =X.ZOEKEN(G2;B1:D1;X.ZOEKEN(G1;A2:A10;B2:D10)).

  • De binnenste X.ZOEKEN zoekt de koffiesoort op in de kolom product en retourneert een rij met de drie prijzen.

  • De buitenste X.ZOEKEN vindt de juiste grootte en retourneert de overeenkomstige prijs.

8.9 Wiskundige matrixfuncties

Met name in de lineaire algebra worden veelvuldig rekenkundige bewerkingen met matrices uitgevoerd. Excel biedt daarvoor ondersteuning met een paar specifieke functies. Het gebruik van deze functies valt buiten het bestek van dit cursusboek.

EENHEIDMAT
Eenheidsmatrix. Engelstalige functienaam: MUNIT
Retourneert een vierkante eenheidsmatrix voor de opgegeven dimensie. Wordt meestal gebruikt in combinatie met andere matrixfuncties.
PRODUCTMAT
Productmatrix. Engelstalige functienaam: MMULT
Retourneert het matrixproduct van twee matrices.
INVERSEMAT
Inverse matrix. Engelstalige functienaam: MINVERSE
Retourneert de inverse van een matrix. Wordt veel gebruikt om stelsels van vergelijkingen met meerdere variabelen op te lossen. Het product van een matrix en zijn inverse is de eenheidsmatrix.
DETERMINANTMAT
Determinant. Engelstalige functienaam: MDETERM
Berekent de determinant van een matrix. Wordt gebruikt bij het oplossen van stelsels vergelijkingen met meerdere variabelen.

8.10 Opgaven

Oefening 8.1 Matrixoptelling (matr001)

Voer de volgende optelling uit met behulp van de Excel matrix methode.

Oefening 8.2 Storingen per district (matr002)

Het nutsbedrijf van een stad houdt een lijst bij waarin per district de gemelde storingen aan gas, water en electra worden vermeld. In de volgende afbeelding is deze lijst te zien. De leiding van het bedrijf wil graag een overzicht van het totaal aantal storingen per district zoals onder Samenvatting berekend. Dit gaat het eenvoudigst met matrixformules.

Bestand: Matr002.xlsx

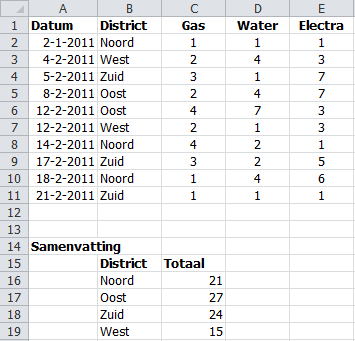
Voer in het werkblad de matrixformules in de cellen C16, C17, C18 en C19 in om het totaal aantal storingen per district te berekenen.

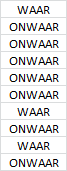
  1. De formule (B2:B11)=B16 levert een matrixkolom van 10 rijen. Als de waarde in een cel uit de reeks B2:B11 gelijk is aan de waarde in cel B16 (= Noord), dan is de waarde in de matrix gelijk aan WAAR (=1) en anders ONWAAR (=0).

  1. Door deze kolommatrix te vermenigvuldigen met de matrix {C2:E11} krijg je een nieuwe matrix van 10 rijen en 3 kolommen. De cellen in de rijen die met ONWAAR worden vermenigvuldigd bevatten allemaal een nul. De cellen in de rijen die met WAAR worden vermenigvuldigd behouden de oorspronkelijke waarden:

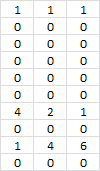
  1. Door hiervan de som te bepalen krijg je het totaal aantal storingen voor het district NOORD.

Oefening 8.3 Willekeurige gehele getallen (matr003)

Met de functie ASELECT.MATRIX kun je willekeurige getallen genereren. Om hiermee te experimenteren en het gedrag van het dynamische matrixformules te bestuderen maak je een nieuw bestand met de volgende gegevens:

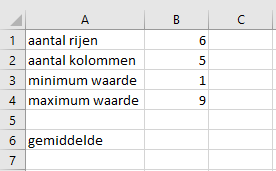
  1. Voer in cel B7 de formule in om willekeurige gehele getallen te genereren, waarbij je voor de eerste vier argumenten verwijst naar de cellen in B1 t/m B4.
  2. Voer in cel B6 een formule in om het gemiddelde van de gegenereerde getallen te berekenen. Gebruik hierbij een verwijzing naar het overloopgebied.
  3. Experimenteer met andere waarden in de cellen B1 t/m B4. Let er op dat de maximumwaarde niet kleiner dan de minimumwaarde mag zijn.

Oefening 8.4 Willekeurige datums en tijdstippen (matr004)

Datums en tijdstippen worden intern in Excel als een getal opgeslagen. Zo wordt 30-06-2020 18:00:00 intern opgeslagen als 44012,75. Hierin is het deel voor de komma de datum en het deel achter de komma het tijdstip. Omdat je met de functie ASELECT.MATRIX willekeurige getallen kunt genereren, kun je dus hiermee ook datums en tijdstippen genereren. In de figuur hierna zie je een voorbeeld.

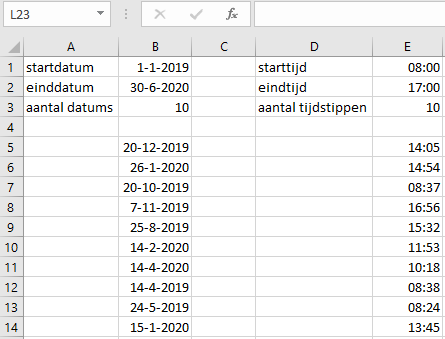
  1. Voer in een nieuw werkblad de gegevens voor de eerste drie rijen in en zorg voor een juiste opmaak.
  2. Voer in cel B5 een formule in om de datums te genereren en in cel E5 een formule om de tijdstippen te genereren. Gebruik hierbij de gegevens in de eerste drie rijen. In de uitvoergebieden moet je zelf de juiste opmaak aanbrengen voor datums of tijdstippen want dat gebeurt niet automatisch.
  3. Experimenteer met verschillende waarden in de eerste drie rijen. Let er op dat de maximumwaarde niet kleiner dan de minimumwaarde mag zijn.

Oefening 8.5 Kolommen sorteren (matr005)

In de figuur hierna zie je de bevolkingsgrootte van de Benelux landen voor achtereenvolgens de jaren 2000, 2005, 2010 en 2015. Wanneer je deze gegevens voor de jaren in omgekeerde volgorde wilt hebben dan kan dat eenvoudig met de dynamische matrixformule SORTEREN waarmee je ook kolommen kunt sorteren.

Bestand: Benelux_Populatie.xlsx

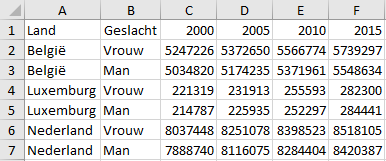
Open het bestand en kopieer de gegevens in de kolommen A en B respectievelijk naar H en I. Voer nu in cel J1 de formule SORTEREN in zodat de gegevens voor de jaren in aflopende volgorde verschijnt. Het resultaat moet er als volgt uitzien.

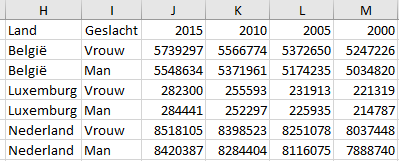
Wanneer je het bestand wilt bewaren, sla het dan op onder de naam [matr005.xlsx` zodat niet het originele bestand gewijzigd wordt.

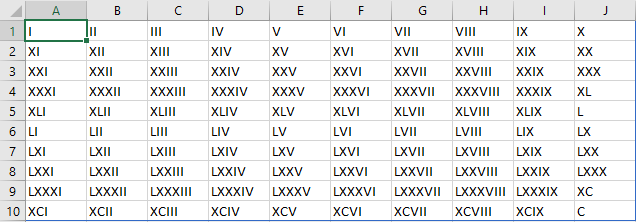
Oefening 8.6 Reeks Romeinse cijfers (matr006)

Maak in een nieuw werkblad een matrix met de cijfers 1 t/m 100 zoals in de volgende figuur.

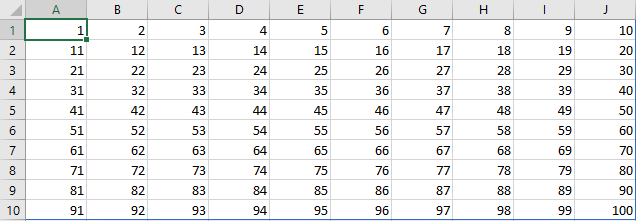
Wijzig daarna de formule zodat je Romeinse cijfers krijgt.

De functie ROMEINS zet Arabische cijfers om naar Romeinse cijfers, als tekst.

Wanneer je het bestand wilt bewaren, sla het dan op onder de naam matr006.xlsx.